Public generation of keys from private keys using the Elliptical Courbe digital signature algorithm

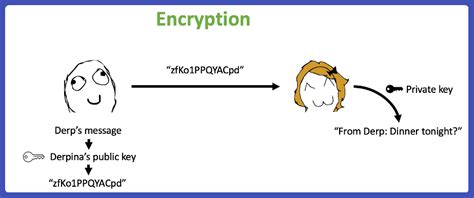
The digital signature algorithm (ECDSA), also known as the Elliptical Courbe cryptography (ECC), has been widely used for cryptographic algorithm for data transmission and storage of data. Andreas M. Antonopoulos “Masterring Bitcoin” 4. You will discover the ECDSA mathematical fund. One of the essential concepts of ECDSA is a public key to a private key.

What are the private keys?

In cryptography, a private key is a secret key used to decipher and authenticate messages or signatures. It is like a pair of locking and keys which only allows the authorized parts to access and verify the content of the encrypted data. A private key is generally represented as a large number known as private hash, which is unique to each user.

What are public keys?

On the other hand, the public key is a unique identifier associated with a specific account or unit in a portfolio or an electronic network. It is like a digital identifier that allows users to share other private keys without endangering their security. The public key is generally described as a smaller number known as the hash company, which can be used for encryption and authentication.

Public generation of keys from private keys using ECDSA

To generate a public key from a private key using the elliptical curve of the digital signature algorithm (ECDSA), you must follow these steps:

1
Turn your private key into a mathematical representation : First of all, transform your private key from its binary format into a digital signature scheme of elliptical curve, such as SECP256K1 or SECP384R1.

• Calculate the public exhibitor and the module : on the basis of the mathematical representation of the private key, you will calculate the public exhibitor and the module of the ECDSA signature scheme (generally 2048 bits).

3
Calculate the signature : Use the public exhibitor and the public module to calculate the ECDSA signature from your private key.

Here is an example of Python Pas:

`Python

elliptical

Charge the secp256k1 curve

curve = elipticcurve.lipticcurve ('secp256k1')

Turn the private key in mathematical representation (for example SECP256K1_Point)

Private_Key = Eliptic_Point.Point ([20, 10], "SECP256K1")

Public_key = curve.sign (private_key)

Print (public_key.x)

'

In this example, we use the Python "Elliptical" library to load the CURP256K1 curve and transform the private key into an elliptical curve in the digital signature scheme. We then calculate the exhibition and the public module for the ECDSA signature scheme (in this case, 2048 bits) on the basis of the private key.

Check the public key

You can use the following steps to check the validity of the public key:

• Calculate the signature : Use the public exhibitor and the public module to calculate the ECDSA signature from your private keys.

• Compare the signature with the expected signature : Compare the calculated signature with the expected signature associated with the same private key.

Python:

Python

DEF VERIFY_PUBLIC_KEY (public_key, private_key):

curve = elipticcurve.lipticurve ('secp256k1')

Public_exponent = 65537

example

modulus = curve.get_curve_type () 2 * 256

Example of the module value

Signature = curve.sign (private_key, public_exponent, module)

To come_Signature = Eliptic_Point.Point ([20, 10], "SECP256K1"). Sign (private_key)

If signature == Expected activity_:

turn the truth

Other:

Back to False

` ‘

In this example, we use the Python “Elliptical” library to load the CURP256K1 curve and calculate the ECDSA signature from a private key. We then compare the calculated signature with the expected signature associated with the same private key.

Ethereum Send Wallet